Problem of the Week
Due Wednesday, Sept. 29, 2021 at 5:00 pm via email to jwswift@gmail.com.
A fictitious species of tree grows in an unusual way. In the first year, the tree grows a trunk which is a square of side length 4 feet. In the second year, a right isosceles triangle grows, attached to the top of the trunk, and two more squares grow at the legs of the right triangle. In the third year, a right isosceles triangle and two squares grow at each leading edge. The figure shows the tree after three years, with the colors showing the growth each year.
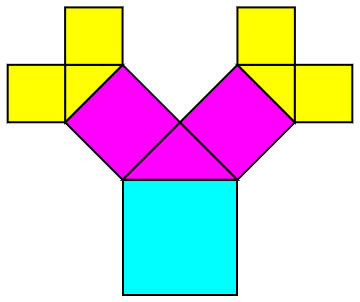
Hint: Use graph paper to sketch the tree.
Rules for Problem of the Week
The contest is open to all undergraduates at Northern Arizona University.
Send your submissions or questions to Jim Swift at jwswift@gmail.com by the due date and time. Please include the subject “potw”. You may attach a pdf (possibly a scan) to the plain text email. No MS Word documents, please. You can use the “TeX for Gmail” extension to get nice equations within email.
The answers should be clearly and logically explained. The goal is to write mathematics, not to to write down the answer and draw a box around it.
If your instructor gives you credit for submissions to problem of the week, please include their name and the class (e.g. Swift, MAT 239).
Problems will be graded on a scale of 1 to 3. A model solution is posted each week. A ladder listing the points earned is posted in the lobby of the Adel Math Building (across from the MAP room). Your name will be printed on the ladder, but no names will be published on the web. Let me know if you want to remain anonymous on the posted ladder.