Problem of the Week
Due Wednesday, Sept. 15, 2021 at 5:00 pm via email to jwswift@gmail.com.
The graph of the function \(f\) is shown.
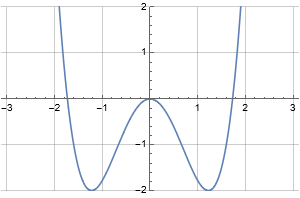
How many solutions to \(f(f(x)) = -2\) are there?
Hint: You do not need to find a formula for \(f\), or the exact value(s) of \(x\) that solve the equation.
Rules for Problem of the Week
The contest is open to all undergraduates at Northern Arizona University.
Send your submissions or questions to Jim Swift at jwswift@gmail.com by the due date and time. Please include the subject “potw”. You may attach a pdf (possily a scan) to the plain text email. No MS Word documents, please. You can use the “TeX for Gmail” extension to get nice equations within email.
The answers should be clearly and logically explained. The goal is to write mathematics, not to to write down the answer and draw a box around it.
If your instructor gives you credit for sumbmissions to problem of the week, please include their name and the class (e.g. Swift, MAT 239).
Solutions are graded out of 3 possible points. A ladder listing the points earned will be posted in the lobby of the Adel Math Building (across from the MAP room). Your name will be printed on the ladder, but no names will be published on the web. Nevertheless, indicate if you want to remain anonymous on the posted ladder.